平成２０年度秋期シスアド問６１－８０解答編

このページは

シスアド

（初級システムアドミニストレータ試験）

の解答と解説のページです。

問題だけで勉強したい方は目次へ戻ってください

問６１	迅速な意思決定、経営責任の明確化を目指し、企業の中に事業領域ごとに独立した仮想的な会社組織を設ける経営組織形態はどれか。

ア	カンパニー制組織
イ	事業部制組織
ウ	プロジェクト組織
エ	持ち株会社

解答	ア

解説	問題中にあるように、小さな仮想的な会社を設ける組織形態をカンパニー（＝会社）制組織といいます。事業部製組織は、開発部・営業部・人事部のように分ける組織形態をいいます。プロジェクト組織は特定の製品などの開発のために一時的に集められる組織形態をいいます。持ち株会社とはホールディング（＝保有）カンパニーともいいほかの会社の株を半数以上保有して子会社にする親会社のことです。

問６２	顧客や市場からの様々な情報を取り込み、その情報を多様な目的で迅速に活用することで顧客との親密な関係を維持し、企業利益の拡大を図る経営手法はどれか。

ア	ＣＲＭ
イ	ＥＲＰ
ウ	ＭＲＰ
エ	ＳＣＭ

解答	ア

解説

４つの用語を以下にまとめます。

ＣＲＭ：（Customer Relationship Management）は、顧客が欲しいサービスや製品を適切に提供して満足してもらい、次も利用してもらえるようにする。ということを目的としています。
ＥＲＰ：（Enterprise Resource Planning）は、経営資源を最適化することを目的とするもので、導入に当たり、さまざまなプロセスの準備（検証・標準化等）が必要となり、専門の部門などにやらせるのが一般的です。
ＭＲＰ：（Material Requirements Planning）とは、資材所要量計画のことで、適切な場所で適切な量（過剰や不足を防ぐ）の在庫を確保するために、発注点や発注量を計算し計画することです。Materialとは資材・物質、Requirementsは必要物、要求という意味です。
ＳＣＭ：（Supply Chain Management）は材料の調達から販売までを最適化することで無駄をなくし、最適な生産を行うという材料販売管理システムです。

問６３	キャッシュフロー計算書において、財務活動によるキャッシュフローに該当するものはどれか。

ア	株式の発行による収入
イ	商品の仕入による支出
ウ	損害賠償金の支払いによる支出
エ	有形固定資産の売却による収入

解答	ア

解説	キャッシュ（＝金）フロー（＝流れ）計算書（Ｃ／Ｓと略したりもされます。）には、営業活動・財務活動・投資活動の３つに分けて記載され、財務活動には株や債権などを記載します。さらに、よく出る用語としては、資産・負債・資本を記述した貸借対照表。また、利益と費用を記載し、儲けや損害を計算したものを損益計算書（Ｐ／Ｌ）。これらを財務諸表といいます。

問６４	損益分岐点に関する記述のうち、適切なものはどれか。

ア	固定費が変わらないとき、変動費率が低くなると損益分岐点は高くなる。
イ	固定費が変わらないとき、変動費率の変化と損益分岐点の変化は正比例する。
ウ	損益分岐点での売上高は、固定費と変動費の和に等しい。
エ	変動費率が変わらないとき、固定費が少なくなると損益分岐点は高くなる。

解答	ウ

解説

各用語がどんな意味をもち、どうやって算出されるのかを下にまとめておきます。

固定費：売上に関係なくかかる費用（例：人経費）
変動費：売上に比例してかかる費用（例：材料費）
変動費率：売上高に対する変動費の割合これは変動費／売上高で算出されます。（変動費＝変動費率×売上高）

利益：企業の儲け
利益 = 売上高－費用

= 売上高－（変動費＋固定費）

= 売上高－（売上高 × 変動費率）－固定費

固定費を移行して、売上高を括弧でくくると
利益＋固定費＝売上高（１－変動費率）

（１ - 変動費率）で両辺を割ると
（利益＋固定費）／（１－変動費率）＝売上高・・・ ①

損益分岐点：損と売上が０つまり、これを上回ると黒字、下回ると赤字という分岐点のことです。
①の式売上高 = (利益＋固定費)／（１－変動費率）の式で売上高＝損益分岐点を代入し、利益が０なので

損益分岐点＝固定費／（１－変動費率）で求めることができます。
この計算式を見ると、損益分岐点では売上＋費用＝０なので、売上高は、固定費と変動費の和に等しいことがわかります。

問６５	商品Ａを先入先出法で評価した場合、当月末の在庫の評価額は何円か。

ア	３，３００
イ	３，４００
ウ	３，６００
エ	３，９００

解答	エ

解説	在庫の合計は１０＋４０＋３０＋１０で９０個。払い出しが３０＋３０で６０個。先入先出法で評価されるので、最後の３０個が残っていることになるので、１０×１１０＋２０×１４０＝１１００＋２８００＝３９００となります。

問６６	決算において、棚卸減耗費として処理するものはどれか。

ア	期中に購入した有価証券の時価が期末に下落している場合
イ	仕入れた商品の時価が期末に下落している場合
ウ	実地棚卸数量が帳簿数量に満たない場合
エ	有形固定資産を定額法で減価償却する場合

解答	ウ

解説	棚卸減耗数量は紙の上での値と実際にある値の差に単価をかけた物で、つまりあるはずなのに無くしてしまったものの額ということになります。また商品の劣化等による評価額の減少を棚卸評価損といいます

問６７	現場改善の５Ｓとは、整理、清潔、清掃、しつけと残り一つはどれか。

ア	信頼
イ	正確
ウ	整とん
エ	整備

解答	ウ

解説	現場改善の５Ｓとは整理、整とん、清潔、清掃、しつけの５つのローマ字の頭文字をとったものです。

問６８	ヒストグラムを説明したものはどれか。

ア	２変数を縦軸と横軸にとり、測定された値を打点し作図して２変数の相関関係を示したもの
イ	管理項目を出現頻度の大きい順に並べた棒グラフとその累積和の折れ線グラフを組み合わせたもの
ウ	データを幾つかの区間に分類し、各区間に属する測定値の度数に比例する面積を長方形を並べたもの
エ	複雑な原因と結果の関係を結び整理して示したもの

解答	ウ

解説	ヒストグラフの例を以下に示します。なお、選択肢アは散布図、選択肢イはパレート図、選択肢エは連関図を表しています。なお、ヒストグラムはＱＣ７つ道具です。

問６９	管理図の利用方法を説明したものはどれか。

ア	作業の前後関係を整理して矢印で表現したネットワーク図を作成し、工程上のボルトネックを発見して日程計画に役立てる。
イ	中央線と上下一対の限界線を引いて、製品などの特性値をプロットし、品質不良や製造工程の異常を検出して不良原因の除去や再発防止に役立てる。
ウ	不良品などの件数や損失金額を原因別に分類し、数値の大きい順に並べてその累積和によって改善効果が高い項目の選定に役立てる。
エ	問題に対し、その原因と考えられる要素との関係を魚の骨のような図に整理し、本質的な原因を追究して解決に役立てる。

解答	イ

解説	管理図はＱＣ７つ道具の１つで、上方管理限界と下方管理限界を設定しその中に収まっているか、偏りがないかなどを調べる管理手法の１つです。以下にその概略例を示します。また、見方ですが、基本的に管理限界内に収まっていれば問題ないのですが、増加・減少の連続的傾向、管理限界付近の連続出現、一方への偏り、周期性の発現などが、あらわれた場合は、管理限界内でも異常と判断します。選択肢アはＰＥＲＴ図，選択肢ウはパレート図，選択肢エは特性要因図（フィッシュボーン）の利用法の説明です。

問７０	プログラムのステップ数が多くなるほどステップ当たりのエラー数も多くなる傾向があるように見受けられたので、データを採って調べた。これを分析するのに最も適した図はどれか。

ア	統計図
イ	散布図
ウ	特性要因図
エ	パレート図

解答	イ

解説	相関関係を導くには散布図を使います。ちなみに、散布図には３つのパターンがあり以下にしめします。最小２乗法などによって直線を求めた場合に、傾き１に近ければ正の相関。傾きが－１に近ければ負の相関となります。

問７１	ある工場でＡ、Ｂを生産している。製品Ａを１トン製造するのに、原料Ｐ、Ｑをそれぞれ４トン、９トン必要とし、製品Ｂについてもそれぞれ８トン、６トン必要とする。また、製品Ａ、Ｂは、１トン当たりそれぞれ２万円、３万円の利益を生む。しかし、原料Ｐは４０トン、Ｑは５４トンしかない。利益を最大にする生産量を求めるために、線形計画問題として定式化されたものはどれか。ここで、製品Ａ、Ｂの生産量をｘ、ｙで表すものとする。

ア	条件 4x+8y≧40 9x+6y≧54 x≧0,y≧0 目的関数 2x+3y → 最大化
イ	条件 4x+8y≦40 9x+6y≦54 x≧0,y≧0 目的関数 2x+3y → 最大化
ウ	条件 4x+9y≦40 8x+6y≦54 x≧0,y≧0 目的関数 2x+3y → 最大化
エ	条件 4x+9y≦2 8x+6y≦3 x≧0,y≧0 目的関数 40x+54y → 最大化

解答	イ

解説

それぞれの原料について考えます。

原料Ｐについて考えると、製品Ａは４トン、製品Ｂは８トン必要で、４０トン以下である必要があります。
よって、４ｘ＋８ｙ≦４０

原料Ｑについて考えると、製品Ａは９トン、製品Ｂは６トン必要で、５４トン以下である必要があります。
よって、９ｘ＋６ｙ≦５４

そして、製造する製品は負になることはありえないので、｢ｘ≧０、ｙ≧０｣となります。
最後に、利益を最大にするので、ｘの利益が２万円、ｙの利益が３万円となるため、｢２ｘ＋３ｙ｣を最大化します。

なお、このような問題を解く手法を線形計画法（ＰＬ法）といい、線形計画法とは、幾つかの制約条件式と目的関数から、最適解を導き出す方法です。以下に例を示します。

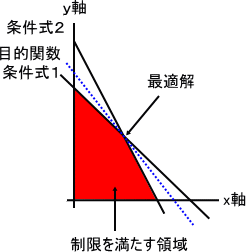画像（問71kai）を表示できません

問７２	表は、あるイベントの準備作業Ａ～Ｅと標準担当者人数及び所要日数の関係を示している。この表に従って準備作業を３５日前に開始したが、ほかの作業との関係で、最初の２０日間は、１人しか担当させられない事態となった。イベントの開催に間に合うように残りの準備作業を行うためには、１日当たり最初何人の担当者を確保する必要があるか。ここで、準備作業に前後関係はなく、どの作業をだれが担当しても生産性は同じであり、何人でも同時に並行して作業ができるものとする。

ア	４
イ	５
ウ	６
エ	７

解答	ウ

解説	まず、トータルの延べ人数を計算します。２×５＋２×５＋３×１０＋２×５＋５×１０＝１１０人月。次に、現在までに消化した量が２０日×１人で２０人月なので、あと１１０－２０＝９０人月残っていることが分かります。残りの日数は３５日－２０日で１５日なので、９０人月÷１５日で６人が答えとなります。

問７３	ＪＩＴ（Just-in-Time）生産方式に関する記述のうち、適切なものはどれか。

ア	需要変化に対して、サイクルタイムをダイナミックに変化させて生産する。
イ	必要なときに必要な量を確保するためにロットを大きくして生産する。
ウ	平準化生産を基本に、各工程を同期させて生産する。
エ	前工程が後工程に作業支持の内容を書いたかんばんを渡しながら生産する。

解答	ウ

解説	ＪＩＴ生産方式は別名トヨタ生産方式、カンバン方式などとも呼ばれ、必要な物を、必要な時に、必要な量だけ生産することで、工程間の中間在庫を減らすことで経済化・効率化を行います。

問７４	定量発注方式における経済的発注量を計算したところ、６００個であった。受注から納期までの調達期間は５日であり、安全在庫量が３０個である場合、この購買品目の発注点は何個か。ここで、１日の平均消費量は５０個であるとする。

ア	２２０
イ	２５０
ウ	２８０
エ	３００

解答	ウ

解説	注文してから届くまでに５日かかり１日で５０個減っていきます。最低でも３０個以上あるようにしなければならないので、５０×５＋３０＝２８０個の時点で発注する必要があるということです。

問７５	ＥＣ（Electronic Commerce）におけるＢｔｏＣに該当するものはどれか。

ア	ＣＡＬＳ
イ	Ｗｅｂ－ＥＤＩ
ウ	バーチャルカンパニー
エ	バーチャルモール

解答	エ

解説	ＥＣ（電子商取引）の形態を以下にまとめておきます。ＢｔｏＢ：企業間での取引ＢｔｏＣ：企業と消費者での取引ＣｔｏＣ：消費者間での取引Ｂはビジネスの略で企業をさし、Ｃはカスタマーの略で消費者を指します。この場合は、企業と消費者での一般的な取引なので、バーチャルモール（インターネット上で商品を買うインターネット取引の形態）が該当します

問７６	ＥＤＩを活用した電子商取引を実施する場合に必要となる取り決めには、取引基本規約、業務運用規約、情報表現規約及び情報伝達規約の四つがある。これらに関する記述のうち、適切なものはどれか。

ア	業務運用規約とは、ＴＣＰ／ＩＰ、ＪＣＡ手順などの通信方法を定めたものである。
イ	情報伝達規約とは、通信回線を介した接続方法を定めたものである。
ウ	情報表現規約とは、システムの運用時間、障害対策などを定めたものである。
エ	取引基本規約とは、データフォーマットを定めたものである。

解答	イ

解説	ＥＤＩ(Electronic Data Interchange)は企業間商取引のことで、取決めには情報伝達規約、情報表現規約、業務運用規約、取引基本規約の４つの取決めがあります。第一レベルの情報伝達規約では、ネットワークの種類や手順を決めます。第二レベルの情報表現規約では、構文ルールなどのフォーマットを取り決めます。第三レベルの業務運用規約では、業務の処理に関する取り決めを行います。第四レベルの取引基本規約では、実際の契約を取り決めます。

問７７	著作権法による保護の対象となるものはどれか。

ア	ソースプログラムそのもの
イ	データ通信のプロトコル
ウ	プログラムに組み込まれたアイディア
エ	プログラムのアルゴリズム

解答	ア

解説	著作権では、ソースプログラムやデータベースは保護の対象内で、プログラム言語やプロトコルは保護の対象になっていません。また、プログラムの複製はバックアップなどにおいてのみ認められています。

問７８	不正競争防止法における営業秘密に該当するものはどれか。

ア	会社役員の個人的なスキャンダル情報
イ	“極秘”の表示をして、広く社内に回覧されている開発中の技術情報
ウ	“社外秘”の表示をして、施錠したロッカーに保管され、公然とは知られていない生産方法に関する情報
エ	当該企業の商品を効果的に販売するための方法が記述された市販書籍

解答	ウ

解説	秘密として管理されている有用な情報であって、公然と知られていないものを営業秘密としているので、広く回覧されていたり市場に出回ったりしているものは営業秘密とはいえません。

問７９	労働派遣法における派遣元の責任はどれか。

ア	派遣先での時間外労働に関する法令上の届出
イ	派遣労働者に指示する業務遂行状況の管理
ウ	労働派遣者の業務遂行に必要となる物資の調達
エ	派遣労働者への休日、休憩時間の適切な付与

解答	ア

解説	労働派遣法における３者の関係を以下にまとめておきます。派遣元が行うのは、届出などで、実際の指揮命令や、休日などは派遣先が責任を負います。

問８０	Ｓ社が備品を購入するとき、購入先のＫ社と図の手順で取引を行っている。この取引手順の中で、売買契約が成立するのはどの地点か。ここで、取引の内容は見積書以降の取引手順を通じて変わらないものとする。

ア	①
イ	②
ウ	③
エ	④

解答	イ

解説	売買契約は、『売り手の売りたいという意志』と『買い手の買いたいという意志』が一致して両者が同意した時点で成立します。選択肢アでは、買いたいという意志を示しただけです。選択肢イでは『売り手の売りたいという意志』で送り返したため、両者が同意したとみなせるので、この時点で売買契約が成立します。

平成２０年度秋期 シスアド 問６１－８０ 解答編

シスアド

平成２０年度秋期シスアド問６１－８０解答編